Iracionální rovnice

• Rovnice s neznámou v odmocněnci (pod odmocnítkem)

Řešte rovnici, kde x ∈ R:

Pokud je v rovnici odmocnina, tak ji odstraníme umocněním celé rovnice – viz rovnice níže.

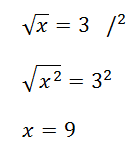
Pokud v rovnici uděláme neekvivalentní úpravu (např. umocnění), tak musíme udělat zkoušku, zda je kořen správný. 

Zkouška:

U zkoušky počítáme pravou a levou část rovnice zvlášť a poté ověříme, zda se rovnají. Pokud se nerovnají, rovnice nemá řešení, pokud se rovnají, tak je kořen rovnice správný.

Místo neznámé dosadíme výsledný kořen rovnice.

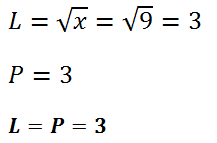
Když zkouška vyšla, tak můžeme řešení rovnice zapsat ve tvaru: K = {a}  – místo a dosadíme kořen rovnice.

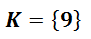
Řešte rovnici, kde x ∈ R:

!POZOR! Pokud chceme rovnici umocňovat kvůli odmocnině, která se nám v rovnici nachází, tak musí být sama na jedné straně rovnice (popř. s další odmocninou) – viz rovnice níže.

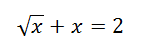
Zde je odmocnina sama na jedné straně rovnice, tak už můžeme celou rovnici umocnit.

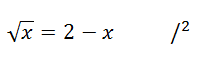
Když se při umocňování rovnice nachází na jedné straně rovnice sčítání nebo odčítání dvou členů (včetně odmocnin!), tak je umocňujeme podle vzorce - (a + b)² nebo (a - b)²!!! V žádném případě je NEumocňujeme každý zvlášť!!! 

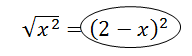
Když nám vyjde výsledek, který se počítá přes kvadratickou rovnici, tak máme dva způsoby řešení. První způsob je dosazení do vzorečku kvadratické rovnice. Druhý způsob je rozklad. Budeme používat způsob druhý, protože je mnohem rychlejší. Pokud nevíte, jak se tímto způsobem počítá, tak se podívejte na kapitolu Rozklady kvadratických trojčlenů, kterou najdete na www.nasprtej.cz. 

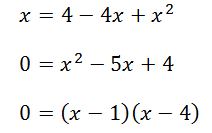
Když máme kořeny rovnice, tak musíme ještě udělat pro oba kořeny zkoušku, protože jsme v rovnici použili neekvivalentní úpravu! 

Zkouška:

U zkoušky počítáme pravou a levou část rovnice zvlášť a poté ověříme, zda se rovnají. Pokud se nerovnají, daný kořen není řešením rovnice, pokud se rovnají, tak je daný kořen řešením rovnice.

Pro x₁:

Místo neznámé dosadíme daný výsledný kořen rovnice.

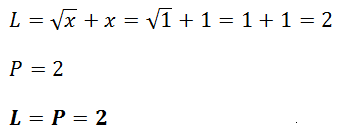
Zkouška platí, tudíž tento kořen patří do celkového řešení rovnice.

Pro x₂:

Místo neznámé dosadíme daný výsledný kořen rovnice.

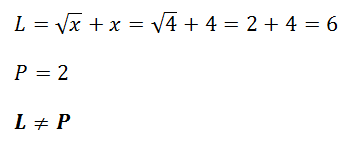
Zkouška neplatí, tudíž tento kořen nepatří do celkového řešení rovnice.

Do celkového řešení patří ta neznámá, které vyšla zkouška. Pokud by zkouška vyšla oběma neznámým, tak řešením budou oba dva body. Když nevyjde zkouška ani u jedné neznámé, tak řešením je prázdná množina (nemá řešení).

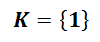
Řešte rovnici, kde x ∈ R:

Když se při umocňování rovnice nachází na jedné straně rovnice sčítání nebo odčítání dvou členů (včetně odmocnin!), tak je umocňujeme podle vzorce:  (a + b)² = a² + 2ab + b² nebo (a - b)2 = a² - 2ab + b²!!! V žádném případě je NEumocňujeme každý zvlášť!!! 

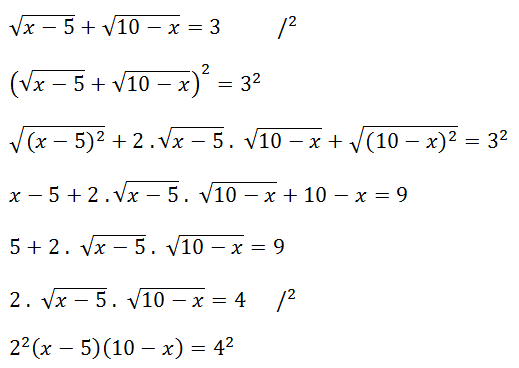
Pro jednodušší výpočet je lepší rovnici vydělit čtyřmi, ale pokud tento krok neuděláme, tak to konečné řešení nezmění! 

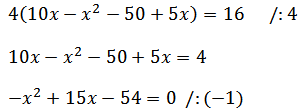
Když máme takto upravenou rovnici, tak nezbývá nic jiného než udělat rozklad nebo dosadit hodnoty do vzorečku kvadratické rovnice.

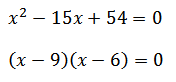
Zkouška:

U zkoušky počítáme pravou a levou část rovnice zvlášť a poté ověříme, zda se rovnají. Pokud se nerovnají, daný kořen není řešením rovnice, pokud se rovnají, tak je daný kořen řešením rovnice.

Pro x₁:

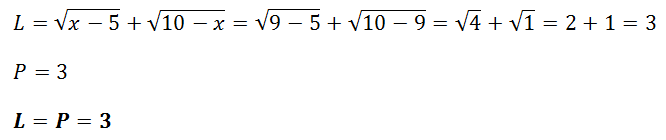
Pro x₂:

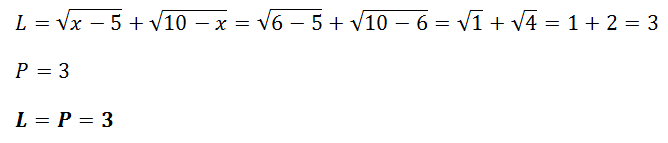
Do celkového řešení patří ta neznámá, které vyšla zkouška. Pokud by zkouška vyšla oběma neznámým, tak řešením budou oba dva body. Když nevyjde zkouška ani u jedné neznámé, tak řešením je prázdná množina (nemá řešení).

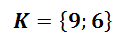
Příklady použity z:

CHARVÁT, Jura; ZHOUF, Jaroslav; BOČEK, Leo. Matematika pro gymnázia : Rovnice a nerovnice. 3. vydání. Praha : Prometheus, 2002. 223 s. ISBN 80-7196-154-X.