Exponenciální rovnice

Obecný tvar: a^x = a^y → x = y

U exponenciálních rovnic vždy potřebujeme, abychom dostali na obou stranách rovnice stejné základy mocnin (a). Toho dosáhneme převrácením zlomků, rozložením, vytknutím, použitím substituce apod. 

Vzorce mocnin

Tyto vzorce již znáte z mocnin, tudíž by neměly činit větší problémy. Jsou velmi důležité pro počítání s rovnicemi, převádíme pomocí nich mocniny do správného tvaru, který už dokážeme vypočítat. 

Příklady

Vždy je důležité dostat stejné základy mocnin, abychom mohli porovnat jejich exponenty, tedy dát exponenty do rovnosti. Vždy si vybereme nějaké číslo, do kterého se budeme snažit dostat výrazy v rovnici. V tomto případě si vybereme například číslo pět, jelikož obě čísla v rovnici mají s ním něco společného. Číslo 25 lze zapsat jako 5² a 1/5 jako 5^-1. Následně pak po upravení již máme na obou stranách rovnice stejné základy mocnin, takže už můžeme dát jejich exponenty do rovnosti, z čehož nám vznikne „obyčejná“ rovnice, kterou už zvládne každý vypočítat.

Výsledek rovnice zapisujeme ve tvaru - K = {a} – kde místo a dosadíme výsledný kořen (kořeny) rovnice. 

U o trochu těžších příkladů je zapotřebí použití substituce. Obvykle se používá u případů, kde se nachází v rovnici tvar kvadratické rovnice, tedy ax² + bx + c = 0, především je důležitý exponent dva nad neznámou x. Pokud bude v rovnici takovýto tvar jako v tomto případě, pak se bude skoro vždy řešit pomocí substituce. Pokud nebudete vědět, jak v nějakém příkladu dále postupovat, tak zkuste substituci – viz rovnice níže. Zvolíme si tedy nějakou substituci a tu dosadíme do rovnice. Obvykle poté vznikne kvadratická rovnice. Výsledné kořeny kvadratické rovnice NEjsou řešením exponenciální rovnice, nýbrž substituce. Je velmi důležité výsledné kořeny dosadit zpátky do námi zvolené substituce za neznámou y. Poté už jsou vypočítané kořeny celkovým řešení exponenciální rovnice.

Příklad níže se vám může zdát jako velmi obtížný, ale není tomu tak, jen jsou v něm použity vzorečky pro mocniny, tedy proto je velmi důležité je znát. V takových to rovnicích když se nepoužije substituce, tak se bude něco vytýkat, a proto je zapotřebí se dostat k takovému tvaru, aby šla neznámá lehce vytknout. Možná se vám z počátku bude zdát, že jste udělali někde chybu, ale příklady jsou stavěné tak, aby vždy vyšly v relativně hezkých číslech, proto neztrácejte v polovině příkladu hlavu a pokuste se vše v klidu dopočítat a především vytknout neznámou a dostat stejné základy mocnin.

Nejdříve rozdělíme exponenty tak, aby v exponentu zůstala pouze neznámá (může obsahovat i číslo, pokud se nám to hodí). Následně vytkneme základ mocnin s neznámou v exponentu. Poté základy mocnin, které mají v exponentu neznámou, převedeme na jednu stranu a zbytek na stranu druhou. Následně rozložíme, abychom dostali stejné základy mocnin. Když budeme mít stejné základy mocnin, tak pak můžeme porovnat jejich exponenty, čímž nám vyjde jednoduchá rovnice.

Výsledek rovnice zapisujeme ve tvaru - K = {a} – kde místo a dosadíme výsledný kořen (kořeny) rovnice. 

V tomto případě je potřeba, aby neznámá s jedničkou v exponentu u čísla 3 byla sama v exponentu, toho docílíme tak, že pomocí vzorečku a^r . a^s = a^r+s rozložíme základ mocniny. Poté vytkneme výraz s neznámou v exponentu. Následně vydělíme celou rovnici tím, co zbylo po vytknutí. Pak převedeme na stejné základy mocnin, a potom dáme do rovnosti exponenty, čímž dostaneme požadovaný výsledek.

Pro tento případ rovnice je potřeba znát logaritmickou rovnici, protože zde nelze dát na obou stranách rovnice stejný základ mocniny, proto ho musíme tzv. zlogaritmovat, tzn., že na obě strany rovnice přidáme logaritmus o libovolném základu, zpravidla o základu deset. Poté použijeme vzorec pro logaritmy log_a r^s = s . log_a r, následně pak vyjádříme x, čímž nám vyjde podíl dvou logaritmů. Můžeme je ještě upravit tím, že je dáme do jednoho logaritmu pomocí vzorečku log_a x = (log_b x) / (log_b a). Výsledek číslem není povinný, zjistíte ho pomocí kalkulačky.

V rovnici se nachází logaritmus na druhou, tudíž použijeme substituci. Vytvoříme ji a dosadíme do rovnice. Vznikne nám tak po upravení kvadratická rovnice, ze které po rozložení získáme výsledné kořeny pro substituci. 

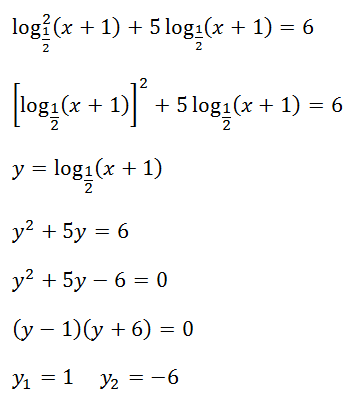
Kořeny dosadíme zpátky do námi zvolené substituce za neznámou y. Výsledkem je kořen celkového řešení této rovnice.

Podmínka

Nakonec musíme ještě určit podmínku tam, kde se nachází neznámá, tedy z argumentu logaritmu. Víme, že argument může být pouze kladné číslo, z čehož vyplývá, že neznámá x musí být větší než mínus jedna – viz podmínka níže.

Výsledek rovnice zapisujeme ve tvaru - K = {a} – kde místo a dosadíme výsledný kořen (kořeny) rovnice. 

Příklady použity z:

PETÁKOVÁ, Jindra. Matematika: příprava k maturitě a k přijímacím zkouškám na vysoké školy. 1. vyd. Praha: Prometheus, 1998, 303 s. Učebnice pro střední školy (Prometheus). ISBN 80-719-6099-3.