
Autor:
Soustava 2 lineárních rovnic o 2 neznámých
3 metody:
a) Sčítací
b) Dosazovací
c) Substituce
Metoda sčítací
Cílem sčítací metody je sečíst 2 rovnice tak, aby se eliminovala (odstranila) jedna neznámá! Vždy se jedna neznámá eliminovat musí!!!
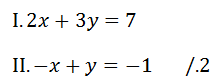
Kterou rovnici sečteme se kterou, si musíme „v hlavě“ vyzkoušet. Rovnice sečteme, popř. některou rovnici vynásobíme, aby se nám jedna neznámá eliminovala!
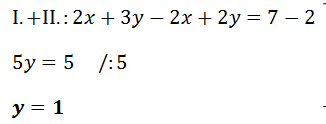
Abychom mohli vypočítat neznámou x, tak do rovnice místoy musíme dosadit kořen y, který nám vyšel.
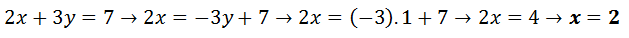
Výsledek zapisujeme ve tvaru: K = {[a; b]} - místo a a b dosadíme řešení, které nám vyšly. Řešení neznámých se do výsledku dávají podle abecedy.
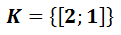
Zkouška
U zkoušky soustavy dvou a více lineárních rovnic stačí, když spočítáme zkoušku u jedné rovnice. Zkoušku spočítáme tak, že počítáme pravou a levou část rovnice zvlášť a poté ověříme, zda se rovnají. Pokud se nerovnají, kořeny rovnice jsou vypočítané špatně, pokud se rovnají, tak jsou kořeny rovnice správné.
Místo neznámých dosadíme výsledné kořeny rovnice.
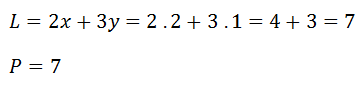
Výsledek zapisujeme ve tvaru: L = P = b - místo b dosadíme řešení, které nám vyšlo ve zkoušce.
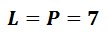
Metoda Dosazovací
Cílem metody dosazovací je vytknutí jedné neznámé z jedné rovnice a dosadit do rovnice druhé – viz rovnice níže.
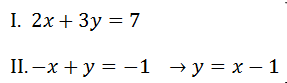
V tomto případě jsme si vyjádřili neznámou y, takže do druhé rovnice dosadíme výsledný výraz místo y – viz rovnice níže.
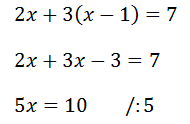
Když máme kořen neznámé, tak ho dosadíme do rovnice, kde jsme si vyjádřili danou neznámou, ale můžeme také dosadit i do první nebo do druhé rovnice v zadání.
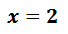
Výsledek zapisujeme ve tvaru: K = {[a; b]} - místo a a b dosadíme řešení, které nám vyšly. Řešení neznámých se do výsledku dávají podle abecedy.
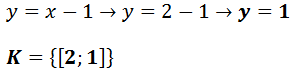
Zkouška
U zkoušky počítáme pravou a levou část rovnice zvlášť a poté ověříme, zda se rovnají. Pokud se nerovnají, kořeny rovnice jsou vypočítané špatně, pokud se rovnají, tak jsou kořeny rovnice správné.
Místo neznámých dosadíme výsledné kořeny rovnice.
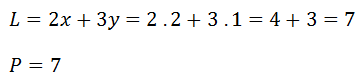
Výsledek zapisujeme ve tvaru: L = P = b - místo b dosadíme řešení, které nám vyšlo ve zkoušce.
Substituce
- Nahrazení výrazu s proměnou jinou proměnou
Pokud máme výraz, který by se těžko počítal sčítací či dosazovací metodou, tak si můžeme pomoci tzv. substitucí, což je nahrazení výrazu s proměnou jinou proměnou – viz rovnice níže.
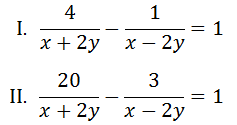
V tomto případě je nejlepší si za a a za b dosadit tyto výrazy. Poté stačí už jen dosadit do rovnice.
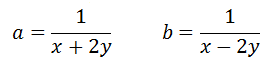
4a je tam proto, že v zadání rovnice je tento výraz v podstatě čtyřikrát, takže proto musí být i 4a. To samé je i u ostatních neznámých.
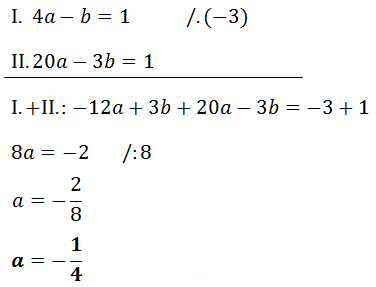
Když dostaneme výsledek, tak ho dosadíme do druhé rovnice, kde jsou výrazya a b.
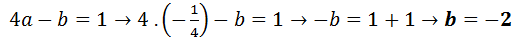
!POZOR! – Výsledky neznámé a ab nejsou konečné kořeny rovnice! Kořeny, které nám vyšly, musíme dosadit do rovnice, kde jsme si vyjádřili a a b – viz rovnice níže.
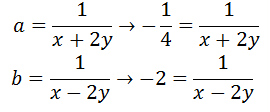
Dostali jsme dvě rovnice, které stačí vynásobit společným jmenovatelem a poté sečíst.
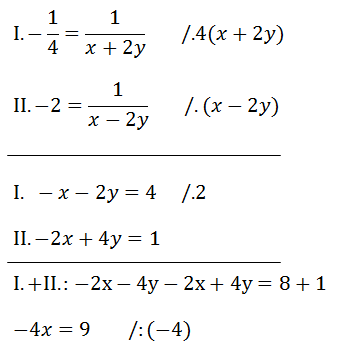
Konečný výsledekx (popř.y) dosadíme do rovnice, kde se nachází x a y (můžeme dosadit třeba i do zadání rovnice).
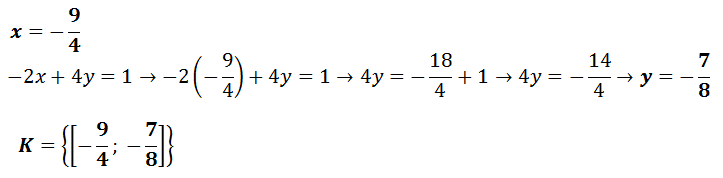
Zkouška
Zkouška se počítá stejným způsobem jako u soustavy lineárních rovnic.
U zkoušky počítáme pravou a levou část rovnice zvlášť a poté ověříme, zda se rovnají. Pokud se nerovnají, kořeny rovnice jsou vypočítané špatně, pokud se rovnají, tak jsou kořeny rovnice správné.
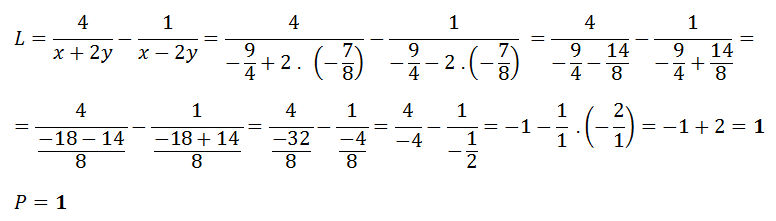
Výsledek zapisujeme ve tvaru:L = P = b - místo b dosadíme řešení, které nám vyšlo ve zkoušce.
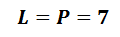
Nekonečně mnoho řešení:
Najděte kořen rovnice, kde x ∈ R
Zde není nic neobyčejného. Máme dvě lineární rovnice, které stačí sečíst (popř. můžeme použít i metodu dosazovací).
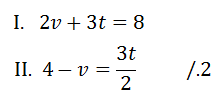
Pokud řešení soustavy lineárních rovnic minimálně o dvou neznámých vyjde jako nekonečně mnoho řešení, tak nestačí pouze napsat výsledek ve tvaru: K = R !!! Musíme ještě určit parametry. První parametr si určíme tak, že jednu neznámou si označíme jako libovolné písmeno (v = a). Druhou neznámou si vyjádříme z první (můžeme i ze druhé) rovnice a místo neznámé, pro kterou jsme si určili parametr, dosadíme zvolené libolné písmeno. Výsledky, které nám vyjdou, zapíšeme ve tvaru K = {[parametr; vyjádřená neznámá]} - viz výsledek níže.
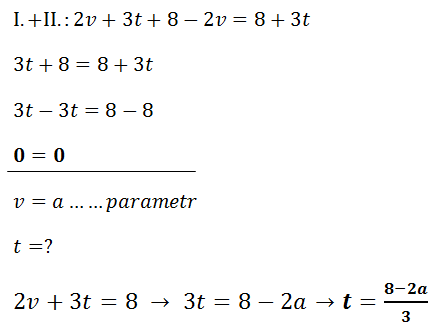
Tento zápis nám v podstatě ulehčuje pozdější vypočítání rovnice, protože když si určíme např. že a = 10, tak po dosazení za druhý kořen hned víme, že v = 10 a t = -4!
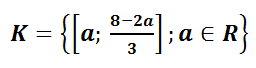
Zkouška
U zkoušky počítáme pravou a levou část rovnice zvlášť a poté ověříme, zda se rovnají. Pokud se nerovnají, kořeny rovnice jsou vypočítané špatně, pokud se rovnají, tak jsou kořeny rovnice správné.
Místo zvoleného parametru (v) dosadíme libovolné číslo, které je z množiny, kde se vyskytují neznámé. Místo druhé neznámé dosadíme vypočítaný kořen s parametrem (viz konečný výsledek výše).
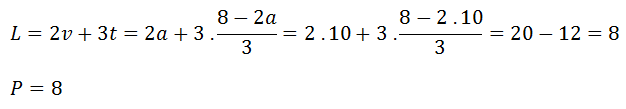
Výsledek zapisujeme ve tvaru:L = P = b - místo b dosadíme řešení, které nám vyšlo ve zkoušce.
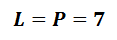
Příklady použity z:
CHARVÁT, Jura; ZHOUF, Jaroslav; BOČEK, Leo. Matematika pro gymnázia : Rovnice a nerovnice. 3. vydání. Praha : Prometheus, 2002. 223 s. ISBN 80-7196-154-X.

Děkuji, moc mi to pomohlo,
Děkuji, moc mi to pomohlo, toto téma pochopit :)
:)
Jsme moc rádi, že ti náš web pomohl :)) Budeme rádi, když o nás dáš vědět dále ;)
Děkuji moc mi to pomohlo
Děkuji,moc mi to pomohlo toto téma pochopit :) :)
děkuji vám moc:)
je to supr naše matikářka neumí vysvětlovat a tak se snažím učivo hledat na internetu a ted už nechodím na jiné str. než tady:)
Poslat nový komentář